|
An algebraic equation is an equation which display style is A=B. Where A and B are equal. It is a uni-variate equation, and it contains only one variable. There are some equations which involve many variables known as a multivariate equation. It is usually approved to an algebraic equation. Such as a{5}-3a+1=0 Definition: When the two expressions plan equal statement called algebraic equation. This statement created a set of variables in the algebraic operations.
This algebraic operation contains adding, reduction, multiplication, and diversion, etc. This type of equation is using for finding one or more roots. As like as a3 + 1 and (y4a2 + 2by – y)/(x – 1) = 12. There is a special case for this type of equations, and that is polynomial equations. The quantity of the solution depends on the number of a degree in this equation. The algebraic equation divided into some variety of equations. They are a Diophantine equation, Linear equation, and quadratic equation. Diophantine equation: All the roots of this type of equations are integers, and its results of interest are also integers. As like as 3a + 7b = 1 or a2 − b2= c3 where a, b, and c are integers. There are three classes Diophantine equations. One has no result, second has many results, and the third one has many results. Such as the equation 6a − 9b = 29 has no result, but the equation 6a − 9b = 30 has a result. There is a method named Congruence methods. This method is helpful for measuring the quantity of solution. With this method, you can find that is this equation can solve or not. Linear equation: A linear equation is a first-degree polynomial. The sum of a set of terms makes this equation. For example- the equation “a + b=5” is a linear equation. With two variables any equation represents a straight line. With a general result, a bundle of equations called simultaneous equations. This result is perfect for both equations. If the result will a=3, b=4, it would show the point (3,4). It is the intersection of two straight lines which presented by the two equations. A linear differential equation is a first-degree algebraic equation. It has a dependent rut and its derivatives. For an example da /db + Ma=L, here M and L can be constants or factors of a, a and b is the independent variable. When M is a constant and L=0, it makes a valuable equation. Quadratic equation: A quadratic equation is a second-degree equation. It has one or more variables. This equation is important for the physics acceleration motion theory. The equation mx2 + nx + p = 0, here m, n, and p are constants and m is not equal to 0. History of the algebraic equation: When mathematics invented then the algebraic equation was also introduced. The Babylonian mathematicians solved some type of quadratic equations at the 2000 BC. It has a very long story. The ancient mathematicians were trying to solve in the method of radical expressions. The Egyptians were able to solve 2-degree equations.
0 Comments
The solution of an algebraic equation is nothing but finding a number or quantity that can balance the equation. The algebra equation is basically a combination of constant value, coefficients, and variables. The total sum of all the quantities given above is equal to zero. The standard form of an algebraic equation is constituted coefficient, one or more than one variable, and the content value. Basically, the algebraic equation denotes a line which is parallel, perpendicular or cuts the X and Y-axis. Some of the algebraic equations types are given below- Linear equations A Linear equation is a type of algebraic equation in which the variable only has degree =1. The linear equitation is denoted as- Y= 5x+8 If we put a single number in place of x, we will get a number of y and vice versa. It is the most common method to solve the linear algebraic equation. Quadratic equation It is also the type of algebra equation which has two higher degrees of a variable. You can better understand the quadratic equation with right example as- y = 2x² + 10x + 8 If we put y = 0, then we will get 2x² + 10x + 8 = 0 Now you can solve the above equation by using the formula method. Also, there are different methods available to solve the equation, but formula method is usually used more than other. Cubic equation The cubic algebraic equation has three higher degrees of a variable. That means you will get three values of a variable. When one of the values of a variable puts on the equation, the equation becomes zero. Hence, you have achieved the right quantity of a variable. Consider an example to understand the cubic equation- 7x³ + 2x² + 10x + 8 = 0 With the specific method, the cubic algebraic equation can be easily solved. Quartic equation with degree = 4 The quadratic equation is a part of the algebraic equation which includes four higher degree variables. Basically, it is simple to solve the as compared to the cubic equation. To better understand the example explains better- It can be solved as the quadratic equation by putting the variable equal to x². Quantic equation Quantic equation includes 5 higher degrees on a variable. It is also taught to solve the quantic equation. You can use various methods to solve this equation which is complicated. Sextic equation It is the algebraic equation that includes 6 higher degree of a variable. The example is given below- Also, there are higher order degrees are available in an algebraic equation, but less than 5-degree algebraic equations are common in algebraic homework.
To get the math help or homework help by the algebra software, you need to visit the proper website. This website includes the program that provides an accurate answer about the variable. You do not need to feel any trouble with solving the algebra equation. The algebraic calculator helps you out with ease. Algebra expression is directly related to the algebraic equations and polynomial equations. In the equation, you have one or more than one unknown, but the values cannot be determined when there is no equation including same unknown. The algebraic equations are most probably used to find the variables values to make both the side equal. For example, you have algebraic equation such as 4x + 8y = 18 And other one is, 3x+ 4y = 14, Now, you have to find the value of x and y respectively. To find the values of unknown, you must know mathematical operations such as addition, subtraction, multiplication, and division. Solve:
To solve this algebra expression, apply subtraction operation on the both. In subtraction, only same variables can subtract. That means the 4x may subtract from 3x and similarly, 8y subtract from 4y. The constant value subtracts from a constant value of other equation. Note that, before subtracting the equation, it needs to make the variables same. That means if we do not make the values same, then we have the equation in which both unknown are available. Then we can never find the value. To avoid this complexity in algebra expression, multiply the number with both the equation. It is not difficult to find the number to multiply in an equation. Find the unknown which you want to eliminate. Then select the number according to it. You want to eliminate x from both the equation then multiply equation one by 3, and another one is 4. Now you have new equations as, 12x + 24y = 54 And, second one becomes, 12x + 16y = 56 Now you have the option to eliminate the variable x from the equation. For this, you need to subtract equation one from two. Then you have a new equation which has only one unknown because the second one has eliminated. You have, 8y = -2, Don’t you worry if you have answered in negative because in algebra expression; you have to face lots of questions that include negative value? It is easy to find the unknown if you have only one unknown. Divide both the side of an equation by 8, and you will get the value of y. You have, y = -1/4 After getting the one variable’s value, you have to find another one. Now put Y’s value on anyone equation in which x is present. Consider equation one, 4x + 8y = 18, When putting the value of y, You have, 4x – 2 = 18 Not transfer the constant value to the right side. Then you have, 4x = 20, Divide both the side by 4, and you have x = 5 In algebra expression, you need to face various difficulties which are solved by considering important factors. The application of algebraic equation helps to know the certain results. To solve the difficult expression, you need to practice more and more. More the practice takes you to be expert in solving the algebraic equations. The basic of algebra is simple but difficult to solve their application. Regular practicing can make you perfect in algebra expression-solving. |
AuthorWrite something about yourself. No need to be fancy, just an overview. Archives
November 2017
Categories
All
|

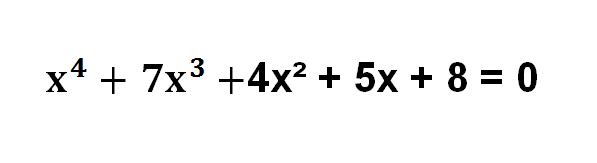
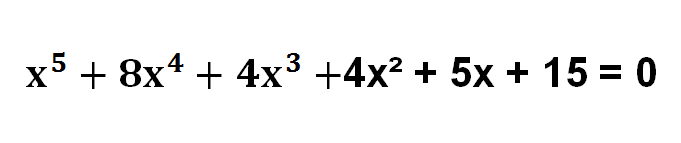
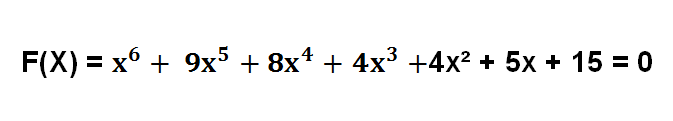
 RSS Feed
RSS Feed
