|
The greatest common factor is the greatest common number if we factorize the two different numbers and multiply them respectively. Therefore after factorizing, the biggest common number between them is the greatest common factor. In other words, the greatest common factor is also known as the highest common factor which is signified by H.C.F. Therefore the procedure goes like this if we factories the number if the two numbers are 10 and 25
Step1-divide the number 10 by 2, and you will get 5 and further divide the number 5 with five till you get 1. Therefore the factors are 2*5*1 Step 2-divide the number 25 by 5, if we factories the number then it will be 5 and five will be further divided by the number 5 and we get 1. Therefore the factors are 5*5*1 Step 3- between the factors 2*5*1 and 5*5*1, the greatest number in common is 5 and thus is called as the greatest common factor. Step 4-Therefore 5 is the greatest common factor or is also known as the HCF or highest common factor. Linear equations- A linear equation is in such a way because a plane is divided into two parts, the X-axis and the Y-axis. If we wish to identify a line regarding mathematics, then we need two variables and a constant and thus the linear equations is designed as ax+by+c=0 where x and y are variables and c is constant. This the generalized equations regarding mathematics which can further become more complex with the passage of time. Therefore this generalize equation will later be used in solving the equations related to complex lines, lines intersecting in between and many more. Therefore let's presume two equations 3x+4y+6=0 and 3x+2y+6=0. Now to solve this equation we will have to apply a mathematical trick, we will first multiply the first equation with 1 and which will yield again 3x=4y=6=0 and the second equation by 2 and we will get 6x+4y+12=0. Now after eliminating both the equation we will get 3x+6=0 and x=-1/2. And now we will put the value of x into the first equation and then we can find the value of y be -15/2 respectively. The entire process can be very exciting if we put the respective values of x and y on the equation we will get the right-hand side value which ultimately defines the value or the position of x and y in the plane sheet. Math help is the best issue when comes to children. You can get the best software when comes to solving mathematical problems as there are much mathematical software. The beautiful part of the software is that it can help solve all the problems in the equations and thus can easily entice people. There are even endless numbers of software which can easily help children learn mathematics. The software includes learning abacus and playing with the calculation and thus finally figuring out the exact value of the question. Thus the significance can’t be overlooked. Mathematics is the very fabric which helps in understanding the very fabric of life and how it’s been made.
0 Comments
Addition and subtraction are the most common mathematical term. Addition and subtraction of two numbers are easy, and each can solve the problem. Instead of it, primary school students feel some difficulties while solving large numerical values. Though students can solve largest numerical subtraction, but they need help while they are solving fractional values. Addition and subtraction of fractional values are quite difficult. Adding and subtracting fractions seems tricky, but you follow simple steps then you need to practice more and more. Here you can find some steps to follow. The adding and subtracting fraction values depends on the denominators. Check if the denominator of all fraction values or same or unequal. If the denominators are not same, then you need to make it equal or find out the LCM of the denominators. If the denominator is similar, then you just need to add the numerator. On the other hand, by making the denominator same, you can add numerator simply. Now, write the numerator after adding or subtracting over the denominator. To understand both the methods, you should have to check some examples below- If the denominator is same, If the denominator is different from another fraction value When the denominator is not same, then you can solve the fractional problem with two different methods. One is using the LCM of a denominator, or another one is a direct method. For example- Here, 12 is the LCM of the denominator. Now, you will get the result as Hence, the LCM method is quite difficult as compared to the direct method because you have to find out LCM first. If using the direct method, you simply need to multiply the numerator of the first fraction to the denominator of second fraction and numerator of the second fraction to the denominator of the first fraction. The example given below that can better help you to understand subtracting fractions. Now, multiply the numerator of the first fraction by the denominator of the second fraction and vice versa then multiply both denominators. You have, Now, you get the solution as It is a simple method as compare of taking the LCM of denominators. Subtracting fractions is basically the simple mathematical problem, but it becomes difficult when there is more than two fractions are available in the problem. When there is more than two fractions are available, then the direct method becomes more complex and LCM method as well. There is no direct trick to solve the complex subtracting fractions.
To overcome the problem, you can buy the software or use the website to solve the fraction values directly. You can find hundreds of websites or software that helps in solving mathematical problems. In the software or website, you just need to fill the problem then press on next step. Either you choose a direct answer or solve the problem step by step. Basically, it is not an online/offline tutorial but the software that helps in solving the adding and subtracting fractions. It is quite simple to use the software. You can buy CD relevant to the software and install on your PC. Now, you can learn how to solve fractions or help others. |
AuthorWrite something about yourself. No need to be fancy, just an overview. Archives
November 2017
Categories
All
|

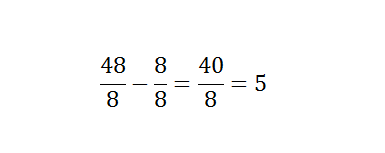
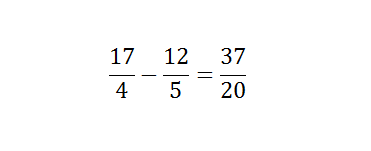
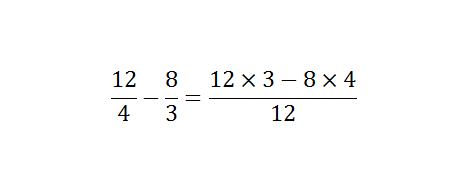
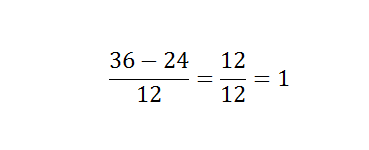
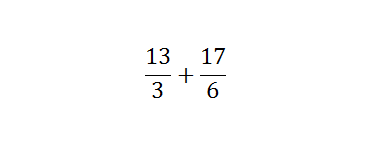
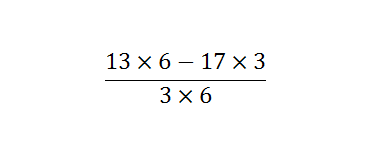
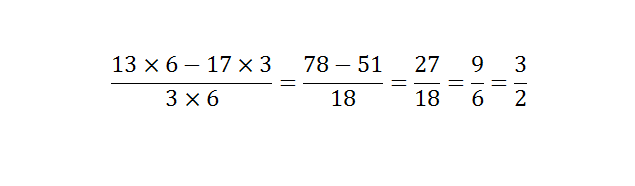
 RSS Feed
RSS Feed
